Bilangan Cacah adalah: Pengertian, Contoh, Manfaat, Sifat, Operasi Hitung

Hai para pembaca setia, pada kesempatan kali ini kita akan membahas mengenai bilangan cacah. Sebelumnya, pasti kalian sudah sering mendengar istilah ini, bukan? Bilangan cacah adalah salah satu jenis bilangan yang sangat penting dan seringkali berguna dalam kehidupan sehari-hari.

Pada dasarnya, bilangan cacah adalah bilangan yang berguna dalam menghitung jumlah atau banyaknya suatu benda atau objek. Bilangan ini terdiri dari angka 0, 1, 2, 3, 4, 5, 6, 7, 8, dan 9. Bilangan cacah dimulai dari angka 0, yang menunjukkan tidak ada benda atau objek yang dihitung.

Penting bagi kita untuk memahami konsep bilangan cacah, karena bilangan ini sangat berguna dalam berbagai situasi dalam kehidupan sehari-hari. Dalam berhitung uang, menghitung jumlah buah-buahan di pasar, atau dalam menghitung jumlah orang yang hadir pada suatu acara, kita membutuhkan bilangan ini.

Selain itu, bilangan cacah juga memiliki sifat-sifat matematika tertentu. Misalnya: sifat komutatif, asosiatif, dan distributif yang sangat berguna dalam operasi hitung. Dalam artikel ini, kita akan membahas lebih lanjut mengenai:

• Pengertian Bilangan Cacah
• Contoh Bilangan Cacah
• Peran Guru dalam Mengajarkan Bilangan Cacah
• Manfaat Bilangan Cacah dalam Matematika
• Sifat-Sifat Operasi Hitung Bilangan Cacah
• Operasi Hitung Bilangan Cacah

Mari kita pelajari bersama-sama dan semoga artikel ini bisa memberikan manfaat bagi kita semua. Selamat membaca!

Pengertian Bilangan Cacah

Bilangan cacah adalah himpunan bilangan yang terdiri dari angka-angka bulat positif, termasuk nol. Notasi matematika untuk bilangan cacah adalah N. Jadi, N adalah himpunan bilangan cacah.

Dalam matematika, bilangan ini sering bermanfaat untuk menghitung jumlah atau banyaknya objek. Misalnya buah-buahan dalam sebuah keranjang, sisi-sisi pada suatu bentuk geometris, atau jumlah kelereng yang anak-anak miliki.

Kita dapat mengurutkan bilangan cacah mulai dari yang terkecil hingga yang terbesar. Bilangan cacah dimulai dari angka: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, dan seterusnya sampai tak hingga.

Setiap penamaan bilangan cacah juga menggunakan nama yang khusus, seperti 1 disebut satu, 2 disebut dua, 3 disebut tiga, dan seterusnya. Untuk angka cacah yang lebih besar, kita menggunakan sistem penamaan yang berbasis sepuluh, seperti puluh, ratus, ribu, juta, dan seterusnya.

Dalam matematika, angka cacah sangat penting dalam berbagai operasi matematika, seperti penjumlahan, pengurangan, perkalian, dan pembagian. 

Dalam pembelajaran matematika, anak-anak akan mulai belajar tentang angka-angka cacah sejak usia dini, di mana mereka akan belajar mengenali angka-angka dari 0 hingga 9, serta konsep dasar matematika, seperti penjumlahan dan pengurangan.

Oleh karena itu, penting bagi anak-anak untuk memahami pengertian bilangan cacah dan konsep matematika dasar lainnya sejak usia dini. Sehingga mereka dapat memperoleh dasar yang kuat dalam matematika dan siap untuk mempelajari konsep matematika yang lebih kompleks di masa depan.

Oleh karena itu, bilangan cacah merupakan konsep matematika dasar yang penting dan perlu memahaminya dengan baik, terutama bagi siswa sekolah dasar. Konsep ini merupakan dasar bagi pemahaman matematika lebih lanjut, seperti operasi hitung pada bilangan negatif dan pecahan.

Tanpa pemahaman yang baik tentang bilangan ini, siswa akan kesulitan dalam memahami konsep matematika yang lebih kompleks.

Contoh Bilangan Cacah

Bilangan cacah merupakan jenis bilangan yang terdiri dari angka 0 dan semua bilangan positif tanpa mempertimbangkan bilangan negatif atau desimal. Dalam bilangan ini terdapat beberapa jenis bilangan, di antaranya adalah bilangan 0, bilangan cacah genap, dan bilangan cacah ganjil.

Bilangan 0

Bilangan 0 adalah angka dasar yang menunjukkan bahwa tidak ada nilai pada suatu bilangan. Dalam notasi matematika, bilangan 0 sering kita lambangkan dengan simbol “0”. Bilangan ini tidak dapat kita anggap sebagai bilangan positif maupun bilangan negatif, sehingga sering kita kenal sebagai “netral”.

Bilangan Cacah Genap

Selain bilangan 0, terdapat pula bilangan cacah genap yang merupakan bilangan yang dapat dibagi habis oleh 2. Dalam notasi matematika, angka cacah genap sering kita lambangkan dengan simbol “2n”, di mana “n” merupakan bilangan bulat. Contoh angka cacah genap antara lain 2, 4, 6, 8, dan seterusnya.

Bilangan Cacah Ganjil

Selain itu, ada juga contoh bilangan cacah ganjil yang merupakan bilangan yang tidak dapat dibagi habis oleh 2. Dalam notasi matematika, angka cacah ganjil sering kita lambangkan dengan simbol “2n+1”, yang mana “n” merupakan bilangan bulat. Contoh angka cacah ganjil antara lain 1, 3, 5, 7, dan seterusnya.

Perbedaan Contoh Bilangan Cacah Genap dan Ganjil

Perbedaan antara contoh bilangan cacah genap dan ganjil juga dapat terlihat dari penulisan notasi desimalnya. Bilangan cacah genap memiliki angka terakhir pada digit satuan yang berupa 0, 2, 4, 6, atau 8, sedangkan angka cacah ganjil memiliki angka terakhir pada digit satuan yang berupa 1, 3, 5, 7, atau 9.

Peran Guru dalam Mengajarkan Bilangan Cacah

Dalam matematika, sistem bilangan cacah merupakan dasar dari semua sistem bilangan yang lebih kompleks, seperti sistem bilangan bulat, pecahan, desimal, biner, oktal, dan heksadesimal.

Oleh karena itu, pemahaman tentang sistem bilangan cacah sangat penting bagi para siswa dalam mempelajari matematika secara keseluruhan.

Dengan demikian, guru harus memastikan bahwa siswa memahami konsep angka cacah dengan baik. Cara memulai mengajarkan angka cacah bisa dengan memberikan contoh konkrit, seperti menunjukkan bilangan pada garis bilangan atau memberikan contoh penggunaan angka cacah dalam kehidupan sehari-hari.

Selanjutnya, guru dapat memberikan siswa sebuah latihan untuk memperkuat pemahaman mereka tentang konsep bilangan ini. Latihan-latihan dapat berupa soal matematika sederhana, permainan, atau aktivitas yang melibatkan angka cacah.

Dalam mengajarkan angka cacah, guru juga dapat menggunakan media pembelajaran yang menarik dan interaktif, seperti video pembelajaran, aplikasi matematika, atau permainan edukatif. Hal ini akan membantu siswa lebih memahami dan tertarik pada konsep angka cacah.

Pada akhirnya, pemahaman yang baik tentang angka cacah akan membantu siswa dalam memahami konsep matematika lebih lanjut dengan lebih mudah. Oleh karena itu, guru harus memastikan bahwa siswa memiliki pemahaman yang kuat tentang konsep sejak dini.

Manfaat Bilangan Cacah dalam Matematika

Salah satu konsep matematika dasar yang harus dipahami adalah bilangan cacah. Bilangan cacah merupakan kumpulan bilangan yang berguna untuk menghitung jumlah benda atau nilai kuantitatif.

Bilangan cacah memiliki manfaat yang sangat penting dalam matematika. Beberapa peran angka cacah dalam matematika antara lain:

1. Sebagai konsep dasar dalam matematika

Bilangan cacah adalah konsep dasar dalam matematika. Dalam matematika, kita memerlukan angka cacah sebagai alat pengukuran atau sebagai dasar dari operasi matematika lainnya, seperti penjumlahan, pengurangan, perkalian, dan pembagian.

Tanpa angka cacah, mungkin tidak akan ada konsep matematika yang lebih kompleks, seperti bilangan pecahan dan bilangan negatif.

2. Manfaat bilangan cacah sebagai alat pengukuran

Bilangan cacah berguna sebagai alat pengukuran dalam banyak situasi. Misalnya, ketika kita ingin mengukur jumlah benda atau barang, kita dapat menggunakan angka sebagai alat pengukurannya. Bilangan cacah juga berguna dalam pengukuran waktu, jarak, dan suhu.

3. Sebagai dasar dari operasi matematika

Bilangan cacah juga berguna sebagai dasar dari operasi matematika seperti penjumlahan, pengurangan, perkalian, dan pembagian.

Operasi matematika ini seringkali berguna dalam kehidupan sehari-hari, seperti ketika kita harus menghitung jumlah uang yang harus kita bayar di kasir atau ketika kita harus membagi jumlah makanan dengan teman kita.

4. Sebagai dasar dari konsep matematika yang lebih kompleks

Bilangan cacah merupakan salah satu sistem bilangan dasar yang sangat berguna dalam matematika. Sistem bilangan ini juga bermanfaat dalam sistem bilangan yang lebih kompleks seperti sistem bilangan biner, oktal, dan heksadesimal.

Tanpa pemahaman yang kuat tentang bilangan ini, sulit untuk memahami konsep matematika yang lebih kompleks.

5. Sebagai alat dalam pemrograman

Bilangan cacah juga berguna sebagai alat dalam pemrograman komputer. Dalam pemrograman, angka cacah sering programer gunakan sebagai variabel atau sebagai nilai pembatas dalam operasi matematika yang kompleks.

6. Manfaat dalam statistik

Bilangan cacah juga sangat penting dalam statistik. Dalam statistik, angka-angka cacah berguna untuk menghitung frekuensi atau jumlah data dalam suatu kumpulan data.

Misalnya, ketika kita menghitung jumlah siswa dalam sebuah kelas, kita menggunakan bilangan ini untuk menghitung jumlah siswa tersebut.

Bilangan cacah juga berguna untuk memodelkan statistik berbagai kejadian dalam kehidupan sehari-hari.

Misalnya, untuk data statistik jumlah penduduk suatu negara atau jumlah kendaraan yang melintas pada jalan tol.

7. Sebagai Dasar dari Bilangan Lainnya

Bilangan cacah merupakan dasar untuk konsep bilangan bulat dan bilangan pecahan. Bilangan bulat adalah bilangan bulat negatif, bilangan cacah, dan nol. Sedangkan bilangan pecahan adalah bilangan yang dapat kita tulis sebagai pecahan, yaitu bilangan yang memiliki pembilang dan penyebut.

Dalam matematika, terdapat kumpulan angka cacah, bilangan bulat, dan bilangan pecahan membentuk himpunan bilangan real yang lengkap. Konsep cacah memainkan peran penting dalam membentuk himpunan bilangan real ini.

8. Menghitung jumlah benda atau nilai kuantitatif

Bilangan cacah berguna untuk menghitung jumlah benda atau nilai kuantitatif. Misalnya, jika ada 5 buah apel, maka kita bisa menggunakan angka cacah 5 untuk menghitung jumlah apel tersebut.

9. Untuk menunjukkan urutan atau posisi

Bilangan cacah juga berguna untuk menunjukkan urutan atau posisi. Misalnya, jika ada 5 orang dalam suatu kelompok, maka kita bisa menggunakan angka-angka cacah 1, 2, 3, 4, dan 5 untuk menunjukkan posisi atau urutan orang tersebut.

Kesimpulan

Dalam matematika,angka cacah memiliki peran yang sangat penting. Bilangan berguna sebagai dasar perhitungan, pengukuran, pemodelan, dan juga sebagai sistem bilangan dasar.

Pemahaman yang baik tentang angka cacah sangat penting bagi pembelajaran matematika yang lebih lanjut. Oleh karena itu, sejak dini anak-anak harus kita ajarkan tentang konsep cacah sebagai dasar matematika.

Sifat-Sifat Operasi Hitung Bilangan Cacah

Bilangan cacah merupakan bilangan bulat positif yang dimulai dari angka 0 hingga tak terhingga. Tanpa kita sadari, konsep perhitungan sangat sering kita gunakan dalam kehidupan sehari-hari dan juga dalam soal-soal matematika. 

Operasi hitung yang menggunakan deretan cacah antara lain penjumlahan, pengurangan, perkalian, dan pembagian. Pada artikel ini, kita akan membahas sifat-sifat dari operasi hitung angka cacah yang perlu anda pahami.

Sifat Penjumlahan Bilangan Cacah beserta Contohnya

Bilangan cacah atau bilangan asli tambah dengan 0 (nol) adalah bilangan yang mulai dari angka 0 dan terus berlanjut tanpa henti ke angka 1, 2, 3, 4, dan seterusnya. Terdapat 4 operasi hitung yang bisa melibatkan bilangan ini, seperti: penjumlahan, pengurangan, perkalian, dan pembagian.

Dalam artikel ini, kita akan membahas sifat-sifat penjumlahan angka cacah beserta contohnya.

Sifat Komutatif

Sifat komutatif berarti penjumlahan bilangan dengan urutan yang berbeda, tidak akanmempengaruhi hasil akhir. Dengan kata lain, jika a dan b adalah angka cacah.

Maka penulisan sifat komutatif angka cacah adalah:

a + b = b + a

 Contoh: 7 + 3 = 3 + 7 = 10.

Sifat Asosiatif

Sifat asosiatif berarti urutan menjumlahkan bilangan dengan urutan yang berbeda, tidak akan mempengaruhi hasil akhir. Dalam hal ini, jika a, b, dan c adalah angka cacah.

Maka:

a + (b + c) = (a + b) + c

Contoh: 2 + (5 + 8) = (2 + 5) + 8 = 6.

Sifat Identitas

Sifat identitas pada penjumlahan bilangan cacah adalah bilangan 0. Dalam hal ini, jika a adalah angka cacah.

Maka:

a + 0 = a

Contoh: 4 + 0 = 4.

Sifat Invers

Sifat invers pada penjumlahan bilangan cacah adalah bilangan negatif yang setara dengan bilangan aslinya. Dalam hal ini, jika a adalah angka cacah.

Maka:

a + (-a) = 0

Contoh: 5 + (-5) = 0.

Sifat Distributif

Sifat distributif berlaku pada perkalian dan penjumlahan angka-angka cacah. Dalam hal ini, jika a, b, dan c adalah angka cacah.

Maka 

a x (b + c) = (a x b) + (a x c)

Contoh: 3 x (2 + 4) = (3 x 2) + (3 x 4) = 18.

Contoh Soal Penerapan Sifat-Sifat Penjumlahan Bilangan Cacah

1. 4 + 5 = 5 + 4 = 9 (Sifat Komutatif)
2. 3 + (4 + 5) = (3 + 4) + 5 = 12 (Sifat Asosiatif)
3. 6 + 0 = 6 (Sifat Identitas)
4. 8 + (-8) = 0 (Sifat Invers)
5. 5 x (3 + 2) = (5 x 3) + (5 x 2) = 25 (Sifat Distributif)

Sifat Pengurangan Bilangan Cacah beserta Contohnya

Dalam matematika, pengurangan bilangan cacah merupakan salah satu operasi dasar yang dalam kehidupan sehari-hari dan dalam matematika. Pengurangan sendiri merupakan operasi yang menghasilkan selisih dari dua angka cacah.

Oleh karena itu, dalam artikel ini akan dibahas tentang sifat-sifat pengurangan angka cacah beserta contohnya yang mudah dipahami.

Tidak Bersifat Komutatif

Komutatif merupakan salah satu sifat operasi matematika yang menunjukkan bahwa operasi kurang dengan urutan yang berbeda, tidak akan mempengaruhi hasil akhirnya.

Dalam hal pengurangan bilangan cacah, sifat komutatif tidak berlaku karena urutan bilangan dapat mempengaruhi hasil akhirnya.

Penulisan secara matematika pengurangan bilangan cacah tidak bersifat komutatif adalah sebagai berikut:

a – b ≠ b – a

Sebagai contoh, jika kita ingin mengurangkan bilangan 5 dengan 3, maka hasilnya adalah 2. Namun, jika kita ingin mengurangkan bilangan 3 dengan 5, maka hasilnya adalah -2. Ini menunjukkan bahwa pengurangan angka cacah tidak bersifat komutatif.

Contoh: 

5 – 3 ≠ 3 – 5

2 ≠ -2

Mari kita lihat contoh-contoh lainnya. Misalkan kita memiliki bilangan 3 dan kita ingin menguranginya dengan 2 terlebih dahulu, maka hasil pengurangannya adalah 1. Namun, jika urutan pengurangan kita ubah menjadi 2 kemudian kita kurangkan dengan 3, maka hasilnya adalah -1.

Contoh:

3 – 2 ≠ 2 – 3

1 ≠  -1

Dari contoh-contoh tersebut, kita dapat melihat bahwa urutan pengurangan sangat mempengaruhi hasil akhir dari operasi pengurangan angka cacah. 

Oleh karena itu, kita dapat menyimpulkan bahwa pengurangan bilangan cacah tidak bersifat komutatif.

Sifat Tidak Asosiatif

Nah, sekarang kita akan membahas tentang sifat pengurangan angka cacah yang tidak bersifat asosiatif. Artinya, operasi hitung pengurangan dengan pengelompokan berbeda akan memberikan hasil yang berbeda.

Definisi operasi pengurangan angka cacah tidak bersifat asosiatif adalah sebagai berikut:

(a – b) – c ≠ a – (b – c)

Contohnya seperti ini: 

Misalkan kita memiliki tiga bilangan cacah, yaitu 9, 4, dan 3. Jika kita ingin mengurangi 9 dengan 4 terlebih dahulu, maka hasilnya akan menjadi 5. 

Kemudian, jika kita mengurangkan 5 dengan 3. Maka hasilnya akan menjadi 2. Dalam notasi matematika, urutan pengurangannya adalah (9 – 4) – 3 = 2.

Namun, jika kita melakukan urutan pengurangan yang berbeda, yaitu dengan mengurangi bilangan 4 dengan 3 terlebih dahulu, maka hasilnya adalah 1. 

Kemudian, jika kita mengurangi bilangan 9 dengan hasil pengurangan yaitu 1. Sehingga hasilnya akan kita dapat adalah 8. Dalam notasi matematika, urutan pengurangannya adalah 9 – (4 – 3) = 1.

Penulisan secara matematika menjadi:

(9 – 4) – 3 ≠ 9 – (4 – 3)

5 – 3 ≠ 9 – 1

2 ≠ 8

Perhatikan bahwa hasil akhir yang kita peroleh berbeda ketika melakukan pengelompokan operasi pengurangan dengan cara yang berbeda. Inilah yang menjadi ciri khas dari sifat pengurangan bilangan cacah yang tidak bersifat asosiatif.

Hal ini bisa menjadi sangat penting ketika melakukan pengurangan dengan tiga atau lebih bilangan. Karena ketika melakukan pengurangan dengan tiga bilangan atau lebih, kita perlu memperhatikan urutan pengurangan yang tepat, agar mendapatkan hasil yang benar.

Itulah penjelasan tentang contoh sifat pengurangan angka cacah yang tidak bersifat asosiatif.

Sifat Distributif

Distributif adalah sebuah sifat matematika penerapan operasi hitung pengurangan dan perkalian pada dua bilangan, akan menghasilkan hasil yang sama, terlepas dari urutan operasi tersebut terjadi. 

Sifat distributif pengurangan angka cacah, hanya berlaku untuk menyebarkan operasi perkalian dan tidak untuk pembagian.

Secara matematika, penulisannya adalah:

 a (b – c) = (a x b) – (a x c)

Mari kita lihat contoh soal yang sudah berikut:

5 (4 – 2) = (5 x 4) – (5 x 2) = 10. 

Pada contoh soal ini, kita memiliki bilangan 5, 4, dan 2. 

Pertama, kita dapat menyelesaikan operasi dalam tanda kurung (4 – 2) yang menghasilkan nilai 2. 

Kemudian, kita dapat mengalikan 5 dengan 4 dan 5 dengan 2, maka menghasilkan berturut-turut bilangan 20 dan 10.

Dari sini, kita dapat menggunakan sifat distributif untuk membuktikan bahwa operasi tersebut benar.

Untuk memulainya, kita dapat mengalikan 5 dengan (4 – 2):

5 (4 – 2) = 5 x 2

Kemudian, kita dapat mengalikan 5 dengan 4 dan 5 dengan 2:

5 x 4 = 20

5 x 2 = 10

Setelah itu, kita bisa menghitung hasil akhir dengan mengurangi hasil dari 5 x 4 dengan 5 x 2:

20 – 10 = 10

Hasil akhirnya adalah 10, seperti yang telah kita peroleh sebelumnya.

Sifat distributif pada pengurangan bilangan cacah sangat berguna dalam penghitungan matematika, terutama ketika terdapat banyak bilangan yang perlu dioperasikan dalam sebuah masalah.

Dengan memahami sifat distributif ini, kita dapat menyelesaikan masalah dengan lebih cepat dan mudah.

Namun, pastikan untuk tetap berhati-hati dan teliti dalam setiap langkah penghitungan, agar hasil akhirnya benar.

Sifat Pengurangan dengan Bilangan yang Sama

Jika pengurangan angka cacah dengan nilai yang sama, maka hasil pengurangan akan selalu nol.

 Artinya:

 a – a = 0

Contohnya: 5 – 5 = 0.

Sifat Identitas

Sifat identitas pada pengurangan menyatakan bahwa ketika pengurangan angka-angka cacah dengan nol. Maka hasilnya akan selalu angka cacah itu sendiri. Artinya, a – 0 = a.

Contohnya: 9 – 0 = 9.

Sifat Pengurangan dengan Bilangan Positif

Jika pengurangan 2 angka cacah, maka hasilnya juga merupakan angka cacah positif. Jika angka pertama lebih besar dari angka kedua.

Artinya: 

A – B = + C, jika A > B

Contohnya: 7 – 3 = 4.

Sifat Pengurangan Bilangan Negatif

Jika pengurangan angka cacah dengan bilangan negatif, maka hasil pengurangan akan bernilai positif.

Artinya:

 A – (-B) = A + B = C

Contohnya: 5 – (-2) = 7.

Sifat Perkalian Bilangan Cacah beserta Contohnya

Perkalian angka cacah adalah salah satu operasi dasar dalam matematika. Dalam operasi ini, perkalian akan terjadi antara bilangan cacah untuk menghasilkan bilangan baru.

Perkalian angka cacah memiliki sifat-sifat khusus yang perlu kita pahami, agar dapat melakukan operasi dengan benar dan efisien.

Berikut adalah penjelasan mengenai sifat-sifat perkalian bilangan ini.

Sifat Komutatif

Sifat komutatif pada perkalian angka cacah menyatakan bahwa urutan bilangan yang terjadi pada perkalian, tidak mempengaruhi hasil perkalian. Artinya, perkalian angka cacah A dan B akan menghasilkan hasil yang sama baik A dikalikan B atau B dikalikan A.

Maka:

A X B = B X A

Contohnya: 12 x 2 = 2 x 12 = 24.

Sifat Asosiatif

Sifat asosiatif pada pengelompokan perkalian dengan cara yang berbeda, tetap akan memperoleh hasil yang sama.

Dalam artian, perkalian angka cacah A, B, dan C akan menghasilkan hasil yang sama jika mengelompokkan dengan cara yang beda.

(A x B) x C = A x (B x C)

Contohnya, (8 x 13) x 4 = 8 x (13 x 4) = 416.

Sifat Distributif

Sifat distributif pada perkalian bilangan cacah menyatakan bahwa perkalian angka cacah dengan jumlah lebih dari satu dapat dipisahkan ke dalam perkalian angka cacah yang lebih kecil.

Artinya, perkalian angka cacah A dengan jumlah B + C sama dengan hasil penjumlahan dari perkalian A x B dan A x C.

Secara matematika, dapat kita simbolkan dengan:

A x (B + C) = (A x B) + (A x C)

Contohnya: 

7 x (9 + 4) = (7 x 9) + (7 x 4)

7 x 13 = 63 + 28

91 = 91

Sifat Identitas

Sifat identitas pada perkalian bilangan cacah menyatakan bahwa perkalian angka cacah dengan satu akan menghasilkan angka cacah itu sendiri. Artinya, perkalian angka cacah A dengan satu sama dengan A.

A x 1 = A

Contohnya: 2 x 1 = 2.

Sifat Perkalian dengan Nol

Sifat nol pada perkalian bilangan cacah menyatakan bahwa perkalian angka cacah dengan nol akan selalu menghasilkan nol. Artinya, perkalian angka cacah A dengan nol sama dengan nol.

A x 0 = 0

Contohnya, 2 x 0 = 0.

Sifat-sifat perkalian angka cacah sangat penting dalam matematika. Memahami sifat-sifat tersebut dapat membantu dalam menyelesaikan berbagai masalah matematika dan meningkatkan kemampuan dalam operasi angka cacah.

Oleh karena itu, sebaiknya memahami sifat-sifat tersebut dengan baik dan berlatih mengaplikasikannya dalam berbagai situasi.

Sifat Pembagian Bilangan Cacah beserta Contohnya

Pembagian merupakan salah satu operasi matematika dasar yang sering bermanfaat dalam hidup kita. Operasi pembagian pada angka cacah tidak mempunyai sifat asosiatif, komutatif, maupun distributif. Namun, terdapat beberapa sifat pembagian bilangan cacah yang dapat kita pahami.

Ada beberapa sifat penting dari operasi pembagian angka-angka cacah yang perlu anda pahami, yaitu:

1. Sifat nol dalam pembagian: Untuk setiap angka cacah a, a bukan nol, maka membagikan 0 dengan a sama dengan 0. Sedangkan angka cacah a membagikannya dengan 0 maka tidak terdefinisikan.
2. Pembagian tidak memiliki sifat komutatif: Artinya, urutan bilangan yang dibagi mempengaruhi hasil pembagian. Sebagai contoh, 6 dibagi dengan 2 sama dengan 3, tetapi 2 dibagi dengan 6 sama dengan 1/3.
3. Pembagian tidak memiliki sifat asosiatif: Artinya, pengelompokan bilangan dalam pembagian mempengaruhi hasil pembagian. Sebagai contoh, (6 dibagi dengan 2) dibagi dengan 3 sama dengan 1, tetapi 6 dibagi dengan (2 dibagi dengan 3) sama dengan 9.
4. Sifat pembagian berpasangan: Jika suatu angka cacah a dibagi dengan b dan b tidak sama dengan nol, maka a juga dapat dibagi dengan kelipatan b. Sebagai contoh, jika 12 dibagi dengan 4, maka 12 juga dapat dibagi dengan 2 atau 1.
5. Pembagian tidak bersifat distributif. Dengan demikian, penyebaran angka cacah pada pembagian akan mempengaruhi hasil.

Artinya: 

Pemahaman atas sifat-sifat operasi pembagian angka cacah menjadi penting dalam penggunaan matematika dalam kehidupan sehari-hari.

Operasi Hitung Bilangan Cacah

Operasi bilangan cacah merupakan dasar dari operasi matematika yang melibatkan bilangan bulat dan bilangan pecahan. Bilangan cacah adalah bilangan yang berguna untuk menghitung jumlah benda, jumlah uang, dan lain-lain yang dapat dihitung.

Operasi angka cacah meliputi empat jenis operasi dasar, yaitu penjumlahan, pengurangan, perkalian, dan pembagian. Keempat operasi tersebut sering kita pakai dalam kehidupan sehari-hari untuk menghitung jumlah, mengurangi jumlah, menambah jumlah, dan membagi jumlah.

Dalam artikel ini, akan membahas mengenai operasi angka cacah, termasuk definisi dan contoh penggunaannya dalam kehidupan sehari-hari.

Penjumlahan Bilangan Cacah

Penjumlahan bilangan cacah merupakan operasi matematika dasar yang sangat penting siswa pahami. Dalam operasi ini, terjadi penjumlahan 2 atau lebih bilangan cacah untuk memperoleh hasil penjumlahan.

Pada setiap level pendidikan, penjumlahan angka cacah selalu akan guru ajarkan sebagai salah satu konsep dasar dalam matematika.

Selanjutnya, kita akan membahas secara rinci tentang penjumlahan angka cacah dan cara mengajarkannya dengan efektif kepada siswa.

Konsep Penjumlahan Bilangan Cacah

Penjumlahan bilangan cacah dapat mendefenisikannya sebagai operasi yang berguna untuk menghitung jumlah dari dua atau lebih angka cacah. Operasi ini menggunakan lambang tanda tambah (+). Dalam operasi ini, bilangan yang dihasilkan dari penjumlahan disebut dengan hasil penjumlahan.

a + b = c

Contoh Penjumlahan Bilangan Cacah

Mari kita lihat contoh sederhana tentang penjumlahan bilangan cacah. Misalkan terdapat dua angka cacah yaitu 5 dan 3, dan kita ingin menghitung hasil penjumlahannya. 

Contoh: 5 + 3 = ……. ?

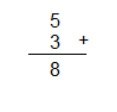
Berikut adalah 5 langkah menjumlahkan bilangan cacah secara vertikal:

1. Letakkan bilangan 5 dan 3 secara vertikal pada bawah tanda tambah (+)
2. Mulai dari angka paling kanan (satuan), lakukan penjumlahan antara dua angka cacah tersebut. Hasilnya adalah 8. Tulis angka 8 pada bawah garis.
3. Lakukan operasi yang sama pada digit berikutnya (puluhan), jika ada. Karena tidak ada angka puluhan pada kedua bilangan, operasi ini tidak perlu terjadi.
4. Lakukan operasi pada digit selanjutnya (ratusan), jika ada. Karena tidak ada angka ratusan pada kedua bilangan, operasi ini tidak perlu melakukannya.
5. Dalam contoh ini, hasil penjumlahan dari 5 dan 3 adalah 8.

Cara Mengajarkan Penjumlahan Bilangan Cacah

Untuk mengajarkan penjumlahan bilangan cacah, guru dapat mengikuti beberapa langkah sebagai berikut:

• Memperkenalkan konsep penjumlahan dan tanda tambah (+). Siswa perlu memahami bahwa tanda tambah (+) berguna untuk menandakan penjumlahan.
• Menunjukkan bagaimana menulis dan membaca penjumlahan angka cacah. Guru dapat memberikan contoh sederhana seperti dalam contoh di atas untuk membantu siswa memahami konsep ini.
• Memberikan latihan berulang-ulang pada penjumlahan angka cacah. Latihan ini dapat siswa lakukan dalam bentuk permainan, cerita, atau gambar untuk membantu siswa lebih memahami dan mengingat konsep penjumlahan dengan mudah.
• Memperkenalkan konsep angka selain angka cacah. Setelah siswa menguasai penjumlahan angka cacah, guru dapat memperkenalkan bilangan pecahan, bilangan negatif, dan bilangan desimal.

Pengurangan Bilangan Cacah

Pengurangan bilangan cacah adalah salah satu konsep dasar matematika yang perlu siswa pahami dengan baik. Sebagai seorang guru, anda akan membantu siswa memahami konsep pengurangan dan cara menghitungnya dengan mudah dan efektif.

Konsep dasar pengurangan angka cacah sangat sederhana. Pengurangan merupakan operasi matematika yang berguna untuk mencari selisih antara dua bilangan.

Pada angka cacah, pengurangan dapat menjelaskannya sebagai operasi untuk menghitung berapa banyak bilangan yang harus menghapus dari bilangan pertama agar memperoleh bilangan kedua.

Sebagai contoh, jika terdapat 5 buah apel dan 2 buah apel kita ambil, maka sisa apel yang tersisa adalah 3. Dalam hal ini, bilangan 5 merupakan bilangan yang akan kita kurangkan dan bilangan 2 merupakan bilangan pengurang atau selisih. Hasil pengurangan tersebut adalah 3.

Penulisan notasi matematika dalam operasi hitung pengurangan sebagai berikut:

a – b = c

Dimana a dan b merupakan bilangan cacah, dan c merupakan selisih antara bilangan a dan b.

Selain memahami konsep dasar pengurangan angka cacah, siswa juga perlu menguasai cara menghitungnya. Ada beberapa cara yang dapat berguna untuk menghitung pengurangan angka cacah, antara lain:

Pengurangan dengan menghitung mundur

Cara ini adalah cara yang paling sederhana dan cocok berguna bagi siswa yang masih belajar. Misalnya, untuk menghitung 8 – 3, kita dapat menghitung mundur dari 8 hingga mencapai angka 3.

Berikut adalah 3 langkah cepat menghitung pengurangan bilangan cacah secara berhitung mundur:

1. Mulai dari bilangan yang lebih besar (8)
2. Kurangi bilangan tersebut dengan bilangan pengurang (3)
3. Terus kurangi bilangan dengan bilangan pengurang sampai mencapai 0

Dalam hal ini, hasil pengurangan adalah 5.

Pengurangan dengan menghitung selisih

Cara ini lebih cepat dan mudah karena tidak perlu menghitung mundur. Misalnya, untuk menghitung 8 – 3, kita dapat mencari selisih antara 3 dan bilangan yang lebih besar dari 3 yang berdekatan, yaitu 5.

Langkah-langkahnya adalah sebagai berikut:

• Cari bilangan yang lebih besar dari bilangan pengurang (3) yang berdekatan (dalam hal ini 5)
• Hitung selisih antara bilangan tersebut dan bilangan pengurang (5 – 3 = 2)
• Hasilnya adalah selisih antara bilangan yang lebih besar dan bilangan pengurang (2)

Pengurangan dengan menghitung secara vertikal

Cara menghitung pengurangan secara vertikal merupakan cara yang cukup efektif dan efisien.

Cara ini bisa dilakukan dengan mengurutkan angka secara vertikal, mulai dari digit yang paling kanan. Selanjutnya, dilakukan pengurangan antara digit yang ada pada kedua bilangan tersebut.

Jika hasil pengurangan antara dua digit tersebut lebih kecil dari nol, maka digit pada digit sebelah kiri akan dikurangi satu.

Digit pada digit sebelah kiri kemudian akan diurutkan kembali secara vertikal dan dilakukan pengurangan kembali. Hal ini akan dilakukan hingga digit pada kedua bilangan sudah habis.

Sebagai contoh, kita akan menghitung 845 – 326 menggunakan cara pengurangan secara vertikal. 

Penjelasan:

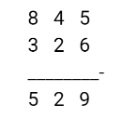
Dalam contoh di atas, kita mulai dengan mengurutkan kedua bilangan secara vertikal, dimulai dari digit paling kanan. 

Selanjutnya, dilakukan pengurangan antara digit 5 dan 6. Karena hasil pengurangan tersebut lebih kecil dari nol, maka digit pada digit sebelah kiri (digit 4) dikurangi satu menjadi 3.

Digit 3 kemudian diurutkan kembali secara vertikal dan dilakukan pengurangan kembali. Hasilnya adalah 9. Kemudian dilakukan pengurangan antara digit 8 dan 3, yang menghasilkan 5.

Dari contoh diatas, kita dapat melihat bahwa cara pengurangan secara vertikal cukup mudah dan efektif untuk kita gunakan. Namun, perlu kami ingatkan bahwa cara ini hanya berlaku untuk pengurangan pada bilangan cacah.

Perkalian Bilangan Cacah

Setelah mempelajari operasi penjumlahan dan pengurangan, siswa akan mempelajari operasi matematika selanjutnya, yaitu perkalian. Perkalian merupakan operasi matematika yang berguna untuk menghitung hasil kali antara dua angka cacah.

Dalam artikel ini, akan dibahas tentang konsep dasar dan cara menghitung perkalian angka cacah dengan mudah dan efektif.

Konsep Dasar Perkalian Bilangan Cacah

Perkalian adalah operasi matematika yang dilakukan untuk menghitung hasil kali antara dua angka cacah. Operasi perkalian pada bilangan cacah dapat dijelaskan sebagai operasi untuk menghitung hasil kali dari dua bilangan yang dikalikan.

Sebagai contoh, jika terdapat 3 kelompok buah-buahan yang masing-masing berisi 4 buah apel, maka total apel yang ada adalah 12 buah. Dalam hal ini, bilangan 3 dan 4 masing-masing merupakan faktor yang akan dikalikan. Hasil perkalian tersebut adalah 12.

Dalam notasi matematika, perkalian dapat dituliskan sebagai berikut:

a x b = c

Dimana a dan b merupakan bilangan cacah, dan c merupakan hasil kali antara bilangan a dan b.

Cara Menghitung Perkalian Bilangan Cacah

Setelah memahami konsep dasar perkalian, selanjutnya adalah mempelajari cara menghitung perkalian angka cacah. Ada beberapa cara yang dapat dilakukan untuk menghitung perkalian angka cacah, di antaranya adalah sebagai berikut:

Perkalian dengan menghitung secara berulang

Cara paling sederhana untuk menghitung perkalian bilangan cacah adalah dengan cara menghitung berulang kali. Misalnya, untuk menghitung 3 x 4, kita dapat menghitung dengan cara menambahkan bilangan 3 sebanyak 4 kali.

Dalam hal ini, langkah-langkahnya adalah sebagai berikut:

Mulai dari bilangan yang pertama (3)

Tambahkan bilangan tersebut dengan bilangan yang sama sebanyak faktor kedua (4)

Dalam hal ini, hasil perkalian adalah 12.

Perkalian dengan Menghitung Secara Vertikal

Untuk memahami konsep perkalian, salah satu cara yang umum kita gunakan adalah dengan cara menghitung secara vertikal. Cara ini dapat membantu siswa untuk lebih mudah memahami konsep perkalian dan menghitung perkalian bilangan cacah dengan lebih cepat dan mudah.

Berikut ini adalah contoh perkalian dengan menghitung secara vertikal:

Misalnya, kita ingin mengalikan dua angka cacah, yaitu 23 dan 5. Langkah-langkahnya adalah sebagai berikut:

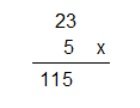
Langkah-langkah:

• Tuliskan bilangan yang akan dikalikan secara vertikal.
• Hitung hasil perkalian pada angka terakhir, yaitu 3 × 5 = 15.
• Tempatkan angka hasil perkalian pada kolom hasil perkalian dan angka sisa pada kolom penyusun bilangan.
• Hitung hasil perkalian pada digit kedua dari kanan, yaitu 2 × 5 = 10. Tambahkan hasil perkalian ini dengan nilai pada kolom hasil perkalian yang lebih kiri. Dalam hal ini, hasil perkalian pada digit kedua dari kanan adalah 10 + 1 = 11.
• Tempatkan angka hasil perkalian pada kolom hasil perkalian dan angka sisa pada kolom penyusun bilangan.
• Hitung hasil perkalian pada digit ketiga dari kanan, yaitu 2 × 0 = 0. Tambahkan hasil perkalian ini dengan nilai pada kolom hasil perkalian yang lebih kiri. Dalam hal ini, hasil perkalian pada digit ketiga dari kanan adalah 0 + 3 = 3.
• Sehingga, hasil perkalian dari 23 dan 5 adalah 115.

Dengan menghitung perkalian secara vertikal, siswa dapat lebih mudah memahami konsep perkalian dan menghitung perkalian angka cacah dengan lebih cepat dan mudah.

Pembagian Bilangan Cacah

Pembagian bilangan cacah merupakan konsep matematika yang penting untuk dipahami. Setelah mempelajari operasi penjumlahan, pengurangan, dan perkalian, pembagian adalah operasi matematika berikutnya yang perlu dipelajari.

Dalam artikel ini, akan dibahas konsep dasar pembagian angka cacah dan cara menghitung pembagian dengan mudah dan efektif. Artikel ini diharapkan dapat membantu siswa dalam memahami konsep matematika dengan lebih baik dan memperbaiki kemampuan berhitung.

Konsep Dasar Pembagian Bilangan Cacah

Pembagian merupakan operasi matematika yang berguna untuk membagi suatu bilangan menjadi beberapa bagian yang sama besar. Dalam notasi matematika, pembagian dituliskan dengan simbol garis miring (/) atau tanda titik dua (::). Contoh penulisan matematika adalah sebagai berikut:

Dalam rumus tersebut, a adalah bilangan yang akan dibagi, b adalah bilangan yang menjadi pembagi, dan c adalah hasil dari pembagian.

Cara Menghitung Pembagian Bilangan Cacah

Setelah memahami konsep dasar pembagian, selanjutnya adalah mempelajari cara menghitung pembagian bilangan cacah. Ada beberapa cara yang dapat kita gunakan untuk menghitung pembagian, di antaranya adalah sebagai berikut:

Pembagian dengan menghitung mundur

Salah satu cara yang paling sederhana untuk menghitung pembagian adalah dengan cara menghitung mundur. Misalnya, untuk menghitung 20 : 4, kita dapat menghitung mundur dari 20 dengan mengurangi bilangan tersebut dengan bilangan pembagi (4) hingga mencapai angka 0.

Dalam hal ini, langkah-langkahnya adalah sebagai berikut:

Mulai dari bilangan yang lebih besar (20)

Bagikan bilangan tersebut dengan bilangan pembagi (4)

Kurangi hasil pembagian dengan bilangan pembagi sampai mencapai 0

Dalam hal ini, hasil pembagian adalah 5.

Pembagian dengan menghitung kelipatan

Cara lain yang dapat kita pakai untuk menghitung pembagian adalah dengan cara menghitung kelipatan. Misalnya, untuk menghitung 20 : 4, kita dapat mencari kelipatan dari bilangan pembagi yang mendekati bilangan yang akan dibagi.

Dalam hal ini, langkah-langkahnya adalah sebagai berikut:

Cari kelipatan dari bilangan pembagi (4) yang mendekati bilangan yang akan dibagi (20)

Dalam hal ini, kelipatan dari 4 yang mendekati bilangan 20 adalah 16 (4 x 4)

Bagi bilangan yang akan dibagi (20) dengan bilangan pembagi (4)

Tambahkan hasil pembagian dengan kelipatan dari bilangan pembagi (16) yang telah dicari sebelumnya

Dalam hal ini, hasil pembagian adalah 5.

Pembagian bilangan cacah dengan menghitung secara vertikal

Pembagian adalah salah satu operasi matematika dasar yang berguna untuk membagi bilangan menjadi bagian yang sama besar.

Cara yang paling umum dalam membagi bilangan cacah adalah dengan cara membagikan secara vertikal.

Dalam artikel ini, akan dijelaskan tentang cara melakukan pembagian dengan menghitung secara vertikal.

Langkah-langkah dalam melakukan pembagian dengan menghitung secara vertikal adalah sebagai berikut:

1. Tuliskan bilangan yang akan dibagi dan bilangan pembaginya secara vertikal. Bilangan yang akan dibagi diletakkan di atas bilangan pembagi.
2. Tentukan berapa kali bilangan pembagi dapat dimasukkan ke dalam bilangan yang akan dibagi. Untuk melakukan ini, cari bilangan yang merupakan kelipatan dari bilangan pembagi terdekat yang kurang dari atau sama dengan bilangan yang akan dibagi. Tuliskan angka tersebut di bawah bilangan yang akan dibagi dan garis lurus di bawah bilangan pembagi.
3. Kalikan bilangan pembagi dengan angka yang dituliskan di bawah bilangan yang akan dibagi. Tuliskan hasil perkaliannya di bawah garis lurus yang telah digambar sebelumnya.
4. Kurangkan hasil perkalian tersebut dari bilangan yang akan dibagi. Tuliskan hasil pengurangan di bawah angka yang telah ditulis di atas garis lurus.
5. Jika masih ada angka yang belum ditempatkan di bawah garis lurus, tarik angka tersebut ke bawah dan letakkan di samping bilangan yang telah dikurangi.
6. Ulangi langkah 2 hingga 4 untuk angka yang telah ditarik ke samping. Tuliskan hasilnya di bawah angka yang telah dikurangi.
7. Ulangi langkah 5 dan 6 hingga tidak ada lagi angka yang belum ditempatkan di bawah garis lurus.
8. Angka yang terletak di atas garis lurus adalah hasil bagi, sedangkan sisa pembagian terletak di sebelah kanan hasil bagi.

Contoh:

Misalkan kita ingin membagi 255 dengan 5 menggunakan metode pembagian secara vertikal.

255 : 5 = …..?

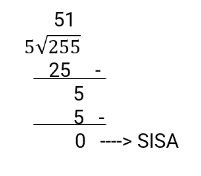
Akhir Kata

Bilangan cacah merupakan jenis bilangan yang terdiri dari bilangan asli dan nol. Angka cacah memiliki berbagai manfaat dan kegunaan dalam kehidupan sehari-hari, seperti dalam pengukuran dan penghitungan. Selain itu, angka memiliki sifat-sifat tertentu, seperti sifat komutatif, asosiatif, dan distributif dalam operasi hitungnya.

Dalam operasi hitung, angka cacah dapat dihitung dengan menggunakan empat operasi dasar, yaitu penjumlahan, pengurangan, perkalian, dan pembagian.

Dalam jenis bilangan cacah, terdapat tiga jenis bilangan yang umum dikenal, yaitu bilangan 0, angka cacah genap, dan angka cacah ganjil. Bilangan 0 memiliki sifat unik sebagai netral dalam operasi penjumlahan dan pengurangan. Sedangkan, angka cacah genap dan ganjil memiliki ciri khas masing-masing dalam angka-angka yang terdapat pada digit terakhirnya.

Dalam penggunaannya, pemahaman terhadap angka cacah dan operasi hitungnya sangat penting untuk diaplikasikan dalam kehidupan sehari-hari. Dengan pemahaman yang baik, angka cacah sangat berguna sebagai alat untuk mengukur dan menghitung, serta sebagai dasar dalam belajar matematika lebih lanjut.